
La relación entre la renta variable (representada por el S&P 500) y la renta fija (bonos del Tesoro a 10 años) ha sido objeto de extensos estudios en el ámbito financiero. Dicha relación puede cambiar en función del nivel de inflación, afectando la estrategia de diversificación de los inversores. Este estudio analiza cómo la correlación entre estos dos activos varía en distintos entornos inflacionarios y si la inflación puede predecir dicha correlación. El periodo que hemos utilizado es desde 1928 hasta 2024.
Para evaluar la relación entre la inflación y la correlación entre renta fija y variable, he empleado un modelo de regresión lineal simple.
Correlación = β0 + β1Inflación + εt
Variable | Descripción |
Correlación | Coeficiente de correlación entre la rentabilidad del S&P 500 y el bono del Tesoro a 10 años en el año t. Se calcula con una ventana móvil de 10 años. |
Inflación | Tasa de inflación anual en porcentaje (%), medida a partir del Índice de Precios al Consumo en el año t. |
Constante (β0) | Valor esperado de la correlación cuando la inflación es 0%. |
Coeficiente de inflación (β1) | Indica el cambio en la correlación entre renta variable y renta fija por cada 1 punto porcentual adicional en la inflación. |
Error (εt) | Captura otros factores no incluidos en el modelo que afectan la correlación. |
Sustituyendo los coeficientes:
Correlación = −0,1686 + 0,0368*Inflación + εt
Variable | Coeficiente | p-value |
Constante (β0) | -0,1686 | - |
Inflación (β1) | 0,0368 | 0,016 |
R-cuadrado | 0,067 | - |
La interpretación de los resultados de las variables del modelo indica que:
• Coeficiente de Inflación (0,0368): por cada punto porcentual de aumento en la inflación, la correlación entre renta variable y renta fija se incrementa en 0,0368. Esto significa que, a medida que la inflación sube, la relación entre ambos activos se vuelve menos negativa, llegando a ser positiva y muy positiva a medida que sigue aumentando.
• Constante (-0,1686): cuando la inflación es 0%, la correlación esperada es de -0,1686, lo que sugiere una ligera inversión de los movimientos de los dos activos.
• R-cuadrado (0,067): la inflación explica el 6,7% de la variabilidad en la correlación, lo que demuestra que existen otros factores que influyen.
• Significancia estadística: el p-value de 0,016 confirma que la relación entre la inflación y la correlación es estadísticamente significativa.
Este modelo simple tiene sus ventajas, como permitirnos evaluar de manera cuantitativa la relación entre la inflación y la correlación de los activos financieros. Además, utilizo datos de casi 100 años, lo que garantiza cierta robustez en los resultados y el modelo es sencillo de interpretar. No obstante, el bajo R2 indica que existen otros factores -política económica, crecimiento, etc.- que influyen en esta correlación. Además, el modelo no captura efectos no lineales (de hecho, en el gráfico veremos una tendencia cuadrática para paliar, en parte, esta deficiencia) y no tiene en cuenta otras variables que sabemos que afectan, como la volatilidad.
El análisis muestra que la inflación tiene un impacto significativo estadísticamente en la relación entre renta variable y renta fija. En entornos de inflación baja, los bonos y las acciones funcionan como activos diversificadores. Sin embargo, a partir de un umbral de 3% de inflación, la correlación se vuelve positiva, indicando que ambos activos pueden verse afectados de manera conjunta por el endurecimiento de la política monetaria.
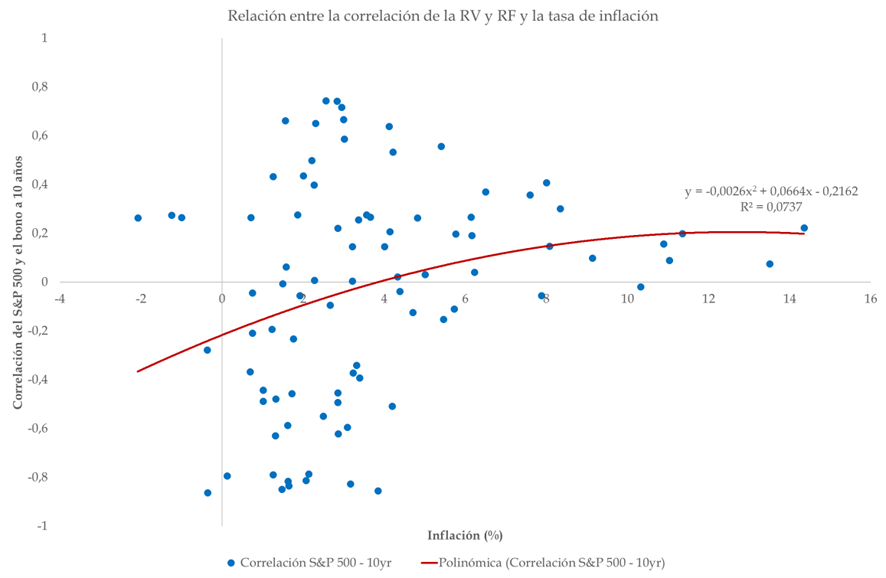
Fuente: Carlos Arenas Laorga
Entonces, ¿la inflación predice la correlación?
Si quieres ver el artículo completo, pincha aquí.

